Lucky Numbers
I first encountered this question as an interview question. Initially I wanted to leave the question as it was after the interview. But after sharing the question with a friend, he was more curious than I was and I ended up joining him for the trip down the rabbit hole.
So without further ado here’s the question.
A lucky number is a number which has the numbers 6 or 8 in its digits. However, if it has both 6 and 8 at the same time, then the number is not lucky.
For example 16, 38, 666 are all lucky numbers while 234 and 687 are not.
Write a program that computes the amount of lucky numbers there are between L and H inclusive where 1 ≤ L ≤ H ≤ 2^62.
Available RAM: 512MB Timeout: 6 seconds
Test Cases:
| L | H | Output |
|---|---|---|
| 1 | 10 | 2 |
| 58 | 72 | 10 |
| 3628 | 3628 | 0 |
| 361,087 | 773,904 | 224,197 |
| 92,871,036,442 | 3,363,728,910,382,456 | 1,160,053,175,781,729 |
| 1 | 1,000,000,000,000,000,000 | 264,160,473,575,034,274 |
Below is the initial code I wrote during the interview. It was a quick and simple brute force method. It didn’t pass the last two test cases as it timeout and was taking too long for numbers above 1,000,000. (All code in this post is written in Python3)
So version 1 (v1) of the code a.k.a. brute force a.k.a. BF is as below.
import sys
import math
lucky = 0
unlucky = 0
array =[]
for num in range (l, h+1):
array = [int(a) for a in str(num)]
if 6 in array or 8 in array:
lucky += 1
if 6 in array and 8 in array:
unlucky += 1
total = lucky - unlucky
print(total)
I didn’t have enough time during the interview to think and had to move on to other questions so I left it as that. Solving about 66% of the problem is usually good enough for most situations in life since life is far from perfect.
But like I said, we jumped down the rabbit hole on this and it took way longer than expected.
The first step in counting faster is to realize that we need to count only the lucky numbers without counting the neutral numbers which would shave off a large chunk of the time without having to iterate through every single number. The problem you face when doing so becomes an accounting nightmare as you will need to make sure that you actually didn’t miss out any number.
The solution was to count the digits using permutation and combinations, looking at the individual digits instead of the entire string of digits.
So version 2 (v2) of the code looked like this:
import sys
import math
print("What is your starting number?")
startNum = int(input("Start: "))
print("What is your ending number?")
endNum = int(input("End: "))
# a function that calculates factorial
def factorial (number):
sum = 1
for i in range(1,number + 1):
sum *= i
return sum
# a function that counts lucky numbers from 0 to a number
# where the number is defined as 1 followed with 0s
def countLuck (numberLength):
count = 0
n = numberLength - 1
# count for the case of 6 in number and double it for 8
for i in range(1,n):
r = n - i
count += 8 ** r * factorial(n) / factorial(r) / factorial(n-r)
count += 1
print (int(count * 2))
countLuck(len(str(endNum)))
Now this code really is quick, shaved off much of the time taken however it could only calculate up to whole numbers starting with the digit 1 and having a string of trailing 0’s. Meaning numbers like 100, 1000, 1,000,000, 100,000,000 etc.
But there was a problem, running the code against the last test case yielded 2 numbers short.
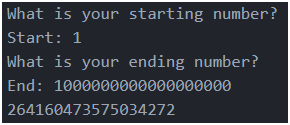
I ignored it thinking that it would sort itself out later. (May not have been the wisest decision)
Part of the reason was that I was preoccupied with solving the other parts of the problem like how do we account for a string of different digits?
So the idea of breaking up a number such as 361087 into its components and counting them came to mind. 361087 = 300,000 + 60,000 + 1000 + 80 + 7
I was happy, I thought I nailed it, I just have to implement the code.
So version 3 (v3) was born. The problem was that the results of BF differed from v3! (By now BF has become the way for us to check if our ‘optimized’ code was correct).
So we continued discussion to try and figure out what we were missing. My friend pointed out to me that I wasn’t accounting for numbers like 360001 which is also lucky! Since my code counted 360001 to 361000 like it was counting 1 to 1000. This was around day 3 of our discussions.
Around day 4, the strategy I took to account for the numbers is to have a counter on whether the digits 6 or 8 have been looped through in the number string. If it has, it would add the remaining string of numbers as lucky and for each digit remaining subtract the unlucky numbers from the count. If a 6 or 8 occured after the number string is lucky, it would then subtract the remaining string of digits as they were now considered unlucky.
Mission accomplished or so I thought. I amended my code happily thinking we’ve nailed it. Remember my not so wise decision of ignoring the 2 missing numbers?
Thus began hours of hair pulling. I could not find the problem with my logic or the code in v2 which I’ve used in v3. We started comparing the results of BF and v2 to try and figure out where the issue was. By the time we crossed the 3 hour mark with no progress, BF started sounding more like a vulgarity to me.
| Number | v2 | BF |
|---|---|---|
| 100 | 34 | 34 |
| 1000 | 434 | 434 |
| 10,000 | 4930 | 4930 |
| 100,000 | 52562 | 52562 |
| 1,000,000 | 538594 | 538594 |
| 10,000,000 | 5371634 | 5371634 |
| 100,000,000 | 52539010 | 52539010 |
| 1,000,000,000 | 506405522 | 506405522 |
| 1,000,000,000,000 | 427420119490 | 427420119490 |
| 1,000,000,000,000,000 | 341413520011634 | 341413520011634 |
| 100,000,000,000,000,000 | 28850763771962640 | 28850763771962642 |
| 1,000,000,000,000,000,000 | 264160473575034272 | 264160473575034274 |
So what we realize was that the deviation occurs at really huge numbers (10^17) and we have no idea why.
I started adding +1 or -1 to the number count and realized that for smaller numbers the total value was affected but for larger numbers there was no change in the digit in the one’s position. I next decided to cast the number into floating point from integer and multiply it by 10 as I was suspecting a rounding off error. I was right, there is a rounding off effect at larger numbers. But the real issue is how do you get it accurately?
I decided to implement the math library for permutations and combinations in python instead of using the short function I wrote. BINGO! problem solved. Though the issue on why that solved the problem even though the logic in my function is perfectly correct is another story for another time. The lesson learnt is:
“Use the library as much as you can, don’t write your own code because you can be wrong even if right!”
Edit
A day after completing v3, it suddenly dawned upon me what was causing the rounding off errors. I learnt about it many years before during my programming lectures in University. Basically fractions causes this issue because base 10 numbers cannot be fully represented as base 2 computations in binary accurately. To solve this in v2 just have to cast the calculation to an integer and not leave it as a floating point value by changing the following line:
count += 8 ** r * int(factorial(n) / factorial(r) / factorial(n-r))
So I tested v2 and the code works fine now as well.
If you are wondering whether I’ll share my code, here is v3 and I hope it is perfect. ![]()
import sys
import math
'''
Conceptually 36589 can be broken down to 30000 + 6000 + 500 + 8 + 9 however
36001 to 36589 was not counted for lucky numbers so we need to account for
the number of digits '6' and '8' appearing when counting. Trailing digits after
a '6' or '8' are lucky while trailing digits after '6' and '8' are unlucky and
should not be counted.
To count lucky numbers for 36589
0 to 30000 add
0 to 6000 add, 589 add
0 to 500 subtract unlucky numbers
0 to 80 subtract unlucky numbers, 9 subtract
so we need:
1. A function that counts the lucky numbers
2. A function that counts unlucky numbers
3. A function that deals with a chunck of lucky numbers e.g. 6000 to 7000
4. A function that deals with a chunck of unlucky numbers e.g 86000 to 87000
'''
print("What is your starting number?")
startNum = int(input("Start: "))
print("What is your ending number?")
endNum = int(input("End: "))
# This function counts lucky numbers from 0 to a number
# where the number is of the format (digit * 10 ** n)
# e.g when counting from 0 to 100, it includes values like 60 and 80
def countLucky (numberLength):
count = 0
if numberLength == 1:
return count
else:
n = numberLength - 1 #First digit is not 6 or 8
# Count lucky numbers
# The number of times '6' appears in the number is denoted by i
for i in range(1, n):
r = n - i
count += 8 ** r * math.comb(n,r)
count += 1 # The case when all digits are lucky except the first
return (count * 2) # Double for lucky number 8
# This function counts unlucky numbers from 0 to a number
# where the number is of the format (digit * 10 ** n)
# Used when the first digit is not 6 or 8
def countUnlucky (numberLength):
count = 0
if numberLength == 1:
return count
else:
n = numberLength - 1
# Count unlucky numbers considering first digit is 6 or 8
for i in range(n):
r = i
count += 9 ** r * math.comb(n,r)
return count
# This function counts lucky numbers in a range
# where the number is of the format (digit * 10 ** n)
# The first digit is 6 or 8
# e.g. 6000 to 7000 or 800 to 900
def rangeOfLucky (numberLength):
count = 0
if numberLength == 1:
return count
else:
n = numberLength - 1
# Count lucky numbers considering first digit is 6 or 8
for i in range(n+1):
r = i
count += 8 ** r * math.comb(n,r)
count -= 1 # not include number like 6000 or 8000
return count
# This function counts unlucky numbers in a range
# where the number is of the format (digit * 10 ** n)
# The first digit is 6 or 8
# e.g. 6000 to 7000 or 800 to 900
def rangeOfUnlucky (numberLength):
count = 0
n = numberLength - 1
count = int('1' + '0' * n) - 1
return count
# This function loops through a number string and count lucky numbers
# from 0 to the number string
def sumLuckyNum (Num):
digits = [int(x) for x in str(Num)]
numLength = len(digits)
count = 0
count6 = 0
count8 = 0
for i in range(numLength):
# if value is 0
if digits[i] == 0:
continue
# if value is less than 6
elif digits[i] < 6 and digits[i] > 0:
if count6 == 0 and count8 == 0:
count += countLucky (numLength - i) * digits[i]
elif count6 > 0 and count8 == 0:
# subtract unlucky numbers, numbers with 8
count -= countUnlucky (numLength - i) * digits[i]
elif count6 == 0 and count8 > 0:
# subtract unlucky numbers, numbers with 6
count -= countUnlucky (numLength - i) * digits[i]
elif count6 > 0 and count8 > 0:
continue
# if value is 6
elif digits[i] == 6:
if count6 == 0 and count8 == 0:
count6 += 1
count += countLucky (numLength - i) * digits[i] # multiply 6 groups
# Add 1 for the number like 6000
count += 1
#Add trailing numbers as they are all lucky
if numLength - i >= 2:
s = [str(j) for j in digits[i+1:]]
trailingNum = int("".join(s)) # this removes leading zeroes
count += trailingNum
elif count6 > 0 and count8 == 0:
count6 += 1
#subtract unlucky numbers, numbers with 8
count -= countUnlucky (numLength - i) * digits[i]
elif count6 == 0 and count8 > 0:
count6 += 1
#subtract unlucky numbers, numbers with 6
count -= countUnlucky (numLength -i) * digits[i]
count -= 1 # subtract for number like 6000
# Subtract unlucky trailing numbers
if numLength - i >= 2:
s = [str(k) for k in digits[i+1:]]
trailingNum = int("".join(s))
count -= trailingNum
elif count6 > 0 and count8 > 0:
count6 += 1
continue
# if value is 7
elif digits[i] == 7:
if count6 == 0 and count8 == 0:
count += countLucky (numLength - i) * (digits[i] - 1) #multiply 7 groups
count+= 1 # for numbers like 60, 600, 6000 etc
# Add the range 6000 to 7000 for example
count += rangeOfLucky(numLength - i)
elif count6 > 0 and count8 == 0:
# subtract unlucky numbers, numbers with 8
count -= countUnlucky (numLength -i) * digits[i]
elif count6 == 0 and count8 > 0:
# subtract unlucky numbers, numbers with 6
count -= countUnlucky (numLength -i) * (digits[i] -1)
count -= rangeOfUnlucky(numLength -i)
count -= 1 ##subtract for number like 6000
elif count6 > 0 and count8 > 0:
continue
# if value is 8
elif digits[i] == 8:
if count6 == 0 and count8 == 0:
count8 += 1
count += countLucky (numLength - i) * (digits[i] - 1) # multiply 7 groups
# Add 1 each for the numbers like 6000 and 8000
count += 2
# Add the range 6*** to 7000 for example
count += rangeOfLucky(numLength - i)
#Add trailing numbers as they are all lucky
if numLength - i >= 2:
s = [str(j) for j in digits[i+1:]]
trailingNum = int("".join(s)) # this removes leading zeroes
count += trailingNum
elif count6 > 0 and count8 == 0:
count8 += 1
# subtract unlucky numbers with 8
count -= countUnlucky (numLength -i) * digits[i]
count -= 1 # subtract for number like 8000
# Subtract unlucky trailing numbers
if numLength - i >= 2:
s = [str(k) for k in digits[i+1:]]
trailingNum = int("".join(s))
count -= trailingNum
elif count6 == 0 and count8 > 0:
count8 += 1
# subtract unlucky numbers, numbers with 6
count -= countUnlucky (numLength -i) * (digits[i] -1)
count -= rangeOfUnlucky (numLength -i)
count -= 1 #subtract for number like 6000
elif count6 > 0 and count8 > 0:
count8 += 1
continue
# if value is 9
elif digits[i] == 9:
if count6 == 0 and count8 == 0:
count += countLucky (numLength - i) * (digits[i] - 2) # multiply 7 groups
# # Add 1 each for the numbers like 6000 and 8000
count += 2
# Add the range 6000 to 7000 and 8000 to 9000 for example
count += rangeOfLucky(numLength - i) * 2
elif count6 > 0 and count8 == 0:
# subtract unlucky numbers, numbers with 8
count -= countUnlucky (numLength -i) * (digits[i] -1)
# subtract for the range 8000 to 9000
count -= rangeOfUnlucky (numLength -i)
count -= 1 # subtract for number like 8000
elif count6 == 0 and count8 > 0:
# subtract unlucky numbers, numbers with 6
count -= countUnlucky (numLength -i) * (digits[i] -1)
# subtract for the range 6000 to 7000
count -= rangeOfUnlucky (numLength -i)
count -= 1 # subtract for number like 6000
elif count6 > 0 and count8 > 0:
count8 += 1
continue
return count
def totalLuck (firstNum, secondNum):
#check if the starting (first) number is lucky or not
digits = [int(x) for x in str(firstNum)]
if 6 in digits and 8 in digits:
total = sumLuckyNum (secondNum) - sumLuckyNum (firstNum)
return total
elif 6 in digits or 8 in digits:
total = sumLuckyNum (secondNum) - sumLuckyNum (firstNum) + 1
return total
else:
total = sumLuckyNum (secondNum) - sumLuckyNum (firstNum)
return total
print (totalLuck (startNum, endNum))